为了求出多元线性回归模型中的参数b0,b1,b2,…,bp,可采用最小二乘法,即在其数学模型所属的函数类中找一个近似的函数,使得这个近似函数在已知的对应数据上尽可能和真实函数接近。
设c0,c1,c2,…,cp分别是b0,b1,b2,…,bp的最小二乘估计,则多元回归方程(即近似函数)为:
y=c0+c1x1+c1x2+
… +cpxp
其中c0,c1,c2,…,cp叫做回归方程的回归系数。对每一组(xi1,xi2,…,xip),由回归方程可以确定一个回归值yi。这个回归值yi与实际观测值yi之差,反映了yi与回归直线
y=c0+c1x1+c1x2+
… +cpxp的偏离程度。若对所有的观测数据,yi与yi
(I=1, 2, …,n)的偏离越小,则认为回归直线与所有试验点拟合得越好。全部观测值yi与回归值yi的偏差平方和为:
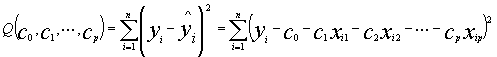
根据微分学中的极值原理c0,c1,c2,…,cp应是下列方程组的解:
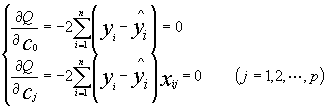
通过整理可将上述方程组写成如下形式:
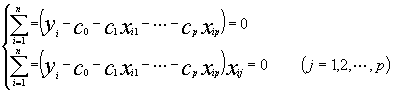
即
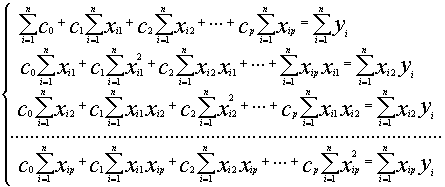
上式也可以用矩阵表示为:
(X'X)C=
X'Y
其中,c=(c0,c1,c2,…,cp)',称为回归方程的系数矩阵,X'是X的转置矩阵。当X'X满秩时,逆矩阵(X'X)-1存在,系数矩阵C可以表示为:
C=
(X'X)-1X'Y
上式即为回归模型中参数B的最小二乘估计。至此,我们就得到了p元线性回归方程。
建立回归方程的目的是要利用它来进行预报与控制。在实际问题中,事先并不能断定随机变量y与x1,x2,…,xp之间确有线性关系,在求解回归方程前,线性回归模型只是一种假设,所以在求出线性回归方程之后,还需对其进行统计检验,给以肯定或否定的结论。有关回归方程及回归系数的显著性检验问题,这里就不介绍了。
|
|